キェ―――
[1]
[2]
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
目指せポール牧
風は秋色
風は秋色
welcome信号
「あのふたりから漂う一種の「色気」」だとよ
マフィアンコミュニティーへの上納金
疲れすぎてると、基本的な倫理観を失いそうになるな


「あのふたりから漂う一種の「色気」」だとよ
マフィアンコミュニティーへの上納金
疲れすぎてると、基本的な倫理観を失いそうになるな
往にし方、そういえば僕は迷路フリークだった。別にやりもしないのに本当に迷路ばかり描いていた。
線画が自由帳のページを埋め尽くしていく過程が好きだったのかもしれない。その趣向は今の自分にも見られるように思う。
クラスの女の子に器用だね、て言われたのを今も覚えている。
その習慣はいつの間にか廃めてしまったわけなのですが、
迷路の生成アルゴリズムというものの存在は前々から気になっていて、やった。
↑のようなものが1秒もかからずに生成されるのである。ブラボー! 一番ありがちな迷路だけど。
飽きなければ、これを自動で解くのも作ってみようかと思う。大体思いつく。
調べていたところ、どうも、粘菌は迷路を最短ルートで解く能力がある(参照)らしい。
リンク先の下のほうの画像がまあまあうける。ていうかそんな発見してどうすんだろう。
この粘菌を作ることを目標としたい。年金納付の延期の手続きは毎年しなければならないんだっけ?
あと、先程のクラスの女の子について、小56くらいだったか、
家庭科の先生の説明を家庭科室の前にあるでかい机のまわりに集まって聞いていたときに後ろから、
抱きついてもいい?、いやでも、という純粋に精神的なエピソードが幾つか思い出され、
非常に可愛かったし、今思うと肉体の発育も目を見張るものがあったが(逆にやらしい表現)、
中3くらいには何故か、どういうわけだかマトモに目を見て話せないレベルの関係になっていた。
だぶん今はキャバクラなどで働いてると思われる。何の話だ。
それはそうと、調べて出てきた4種ほどの方法を試したので、折角だから書いておく。
出来栄えが微妙に違う。若干マニアックな領域である。
1.棒倒し法
上からガーーってランダムに棒を倒す なんでできるかはよく分からない
作るのは最易 完成度低
2.穴掘り法
穴を掘る
ソースと迷路の綺麗さを総合しても一番気に入っているタイプ
3.壁伸ばし法
逆に壁を伸ばす
2.と好みは分かれるかもしれない 違いがわかるだろうか
4.クラスタリング法
クラスタリングをする
スマートにできるかと期待していたらすごい時間がかかった
ソースも冗長 完成度も棒倒し並
しかしいかにも応用幅の広い考え方であるぽい雰囲気を醸す
急に冷めたね俺
久しぶりに、溜まったプログラムについて書こうと思う。アヴェマリアを唄う安部まりあさん並にどうでもいいかもね。
◆魚群

boidsというアルゴリズムを用いた、魚や鳥の群れの動きのシミレーションです。
アルゴリズムって言うほど大した仕組みでもないんだけど、点同士が相互作用をして、
他の点を見つけたら近づき、2点間がちょうどよい距離だったら並走し、近づきすぎたら離れる、ということをやるとできる。
この点がですね、魚ぽく動くのです。
単純なルールの割に見てると本物に近いもので、生物の脳にこういった本能が備わっているというのは面白い。
こういった、単純なルールの割に、っていうのと、
鳥瞰してシミュレート、そして一般性を持つ、みたいのが基本的に好きなのである。
◆魚群2
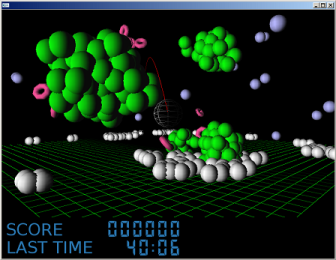
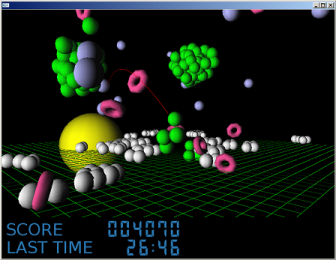
これはシューティングゲームです。
上のは二次元空間上の点で、他のサイトでも同じようなのがいろいろあって面白くなかった。
では、これを三次元に拡張したらどうなるカナーって思ってやったら、きもいやつができた。
その頃、ちょうど学校の文化祭に出すゲームが不足しているとのことだったので、
魚群の動きをする丸いのを打ち落とすシューティングとして採用した。
弾は方位角と仰角という球状極座標の形(分かりやすくいうと地球儀の緯線と経線で位置を決定するような)
で発射方向を決定するということにした。
ミニゲームとしてはまあまあいいできだと思った。
今youtube見たらもっとすごいのがあった。ルールを増やしたのだろう。
いつかも同じようなことを書いたけれど、ずっと考えているのは、
ライフゲームを拡張したようなのをboidsに組み合わせて、自己増殖する生命体を創造したいと目論んでいる。
遺伝的アルゴリズムや人工知能も組み込めれば、と思うがそんなことをしている余裕は無い。
ていうかこれって卒論くらいのレベルの研究で散々やられている気がする。よくは知らない。
この魚群の応用例はいくらでもあると思う。すぐ思いつくのは結晶のでき方、とか。
と、こういった取り留めのない所懐を無意識の中に放り込んで寝かせてある。
◆n次代数方程式の解を求める
学校の課題で、入力された2次方程式の解を求めろ、というものがあって、
それ自体は解の公式に放り込むだけであったので非常にぬるいものであった。
で、それをやっていてn次の代数方程式は解けるのかと思って考えてみた。
調べたところによると、ガロア理論(だったかな?)というものにより、
代数方程式は5次の方程式までしか一般的な解の公式は存在しないということだった。
(余談:5次まで、というこの「5」に何か次元の壁というか大いなる意味があるのか?)
それで少し絶望したが、コンピュータにいろいろ計算させて解を求める方法を思いついた。
たぶんこれも昔からある方法だと思うし、より効率のいい方法も存在しているだろうが、調べたら難しそうだったので深入りしなかった。
大まかには、単調変化が保障された二つの極値の間で、一桁ずつ絞って近似していくということなんだが、
極値を取る定義域の値をどうやって求めるかというところがミソで、
それは、[求めたい関数の微分]=0を満たすxとする必要(十分ではない)があるということである。
つまり、微分して次数が1次下がったの=0となるxを求めればよくて、
さらにそれを求めるには、同じように、と再帰的な操作を行うことで、取り合えずn次から2次まで次数を下げることが出来、
そこからまた一つずつ次数を上げていって詰めて行く、という方法をとったところ、かなりの精度でうまくいった。
でもこれでは複素解は求められない。あまり興味の湧かない話である。
◆弧と弦の長さから半径を求める
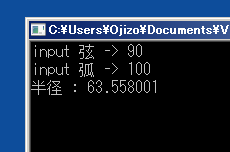
なんとなく丘とかの風景などを見ているとき、この丘は地面の下に埋まっている円弧の一部が現れたものだが、
果たして地面の下に埋まっているこの円の半径はどのくらいなんだろうか?と思ったことは無いだろうか(たぶん、ない)。
まあそんな愚かな問いを発してきた人物がいて、その夢を叶えたのが本プログラムである。
考えていると、sin関数を含んだ代数方程式が出てきて、どうしても解けなかった。
しかし、sinをテーラー展開することでn次代数方程式に帰着することが明らかになる。
ちょうど上のやつを作った後であったため、いきなり応用例が出てきてびっくりしたのを覚えている。
sinの展開の7次くらいまでやるとほとんど正確な値が出てくるのが分かった。
◆割と厳密な単振子
◆割と厳密な二重振子
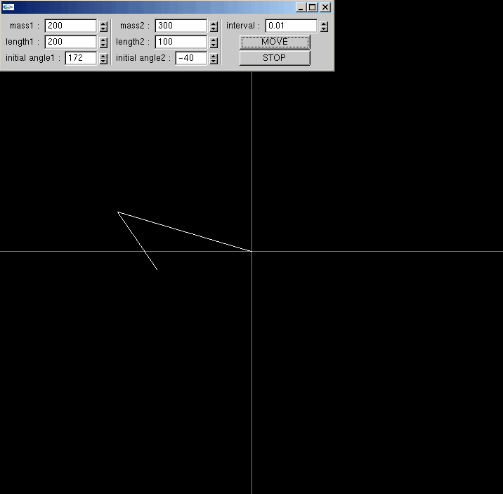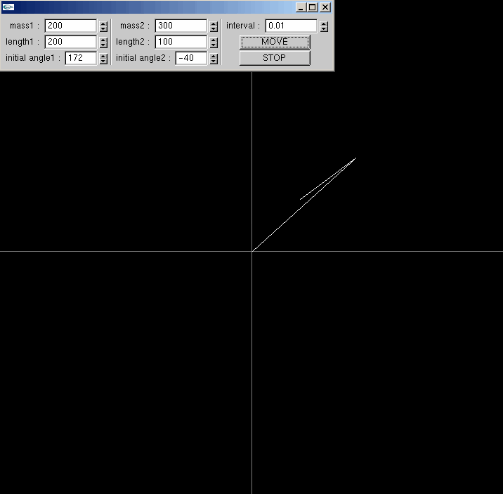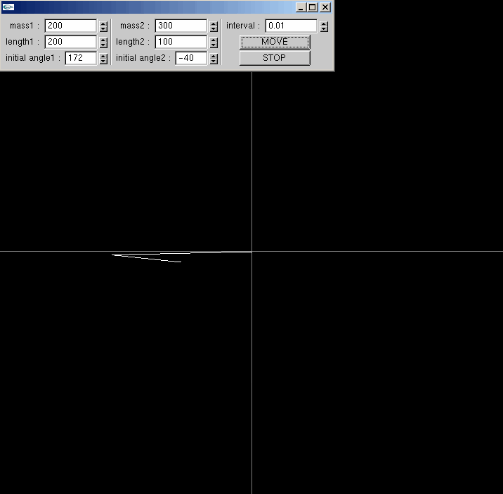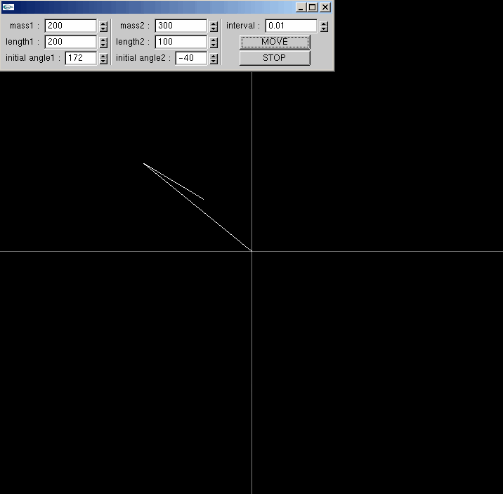
微分方程式を扱うようなプログラムを作りたいナアと思って、真っ先に思いついたのが二重振子であった。
ていうか、この馴れ初めをぐだぐだ書く作業がなんかだるくなったため、もう止めにしようと思う。
二重振子の実験、これみるとなかなか面白いかもしれない。カオス的振る舞い。
◆魚群
boidsというアルゴリズムを用いた、魚や鳥の群れの動きのシミレーションです。
アルゴリズムって言うほど大した仕組みでもないんだけど、点同士が相互作用をして、
他の点を見つけたら近づき、2点間がちょうどよい距離だったら並走し、近づきすぎたら離れる、ということをやるとできる。
この点がですね、魚ぽく動くのです。
単純なルールの割に見てると本物に近いもので、生物の脳にこういった本能が備わっているというのは面白い。
こういった、単純なルールの割に、っていうのと、
鳥瞰してシミュレート、そして一般性を持つ、みたいのが基本的に好きなのである。
◆魚群2
これはシューティングゲームです。
上のは二次元空間上の点で、他のサイトでも同じようなのがいろいろあって面白くなかった。
では、これを三次元に拡張したらどうなるカナーって思ってやったら、きもいやつができた。
その頃、ちょうど学校の文化祭に出すゲームが不足しているとのことだったので、
魚群の動きをする丸いのを打ち落とすシューティングとして採用した。
弾は方位角と仰角という球状極座標の形(分かりやすくいうと地球儀の緯線と経線で位置を決定するような)
で発射方向を決定するということにした。
ミニゲームとしてはまあまあいいできだと思った。
今youtube見たらもっとすごいのがあった。ルールを増やしたのだろう。
いつかも同じようなことを書いたけれど、ずっと考えているのは、
ライフゲームを拡張したようなのをboidsに組み合わせて、自己増殖する生命体を創造したいと目論んでいる。
遺伝的アルゴリズムや人工知能も組み込めれば、と思うがそんなことをしている余裕は無い。
ていうかこれって卒論くらいのレベルの研究で散々やられている気がする。よくは知らない。
この魚群の応用例はいくらでもあると思う。すぐ思いつくのは結晶のでき方、とか。
と、こういった取り留めのない所懐を無意識の中に放り込んで寝かせてある。
◆n次代数方程式の解を求める
学校の課題で、入力された2次方程式の解を求めろ、というものがあって、
それ自体は解の公式に放り込むだけであったので非常にぬるいものであった。
で、それをやっていてn次の代数方程式は解けるのかと思って考えてみた。
調べたところによると、ガロア理論(だったかな?)というものにより、
代数方程式は5次の方程式までしか一般的な解の公式は存在しないということだった。
(余談:5次まで、というこの「5」に何か次元の壁というか大いなる意味があるのか?)
それで少し絶望したが、コンピュータにいろいろ計算させて解を求める方法を思いついた。
たぶんこれも昔からある方法だと思うし、より効率のいい方法も存在しているだろうが、調べたら難しそうだったので深入りしなかった。
大まかには、単調変化が保障された二つの極値の間で、一桁ずつ絞って近似していくということなんだが、
極値を取る定義域の値をどうやって求めるかというところがミソで、
それは、[求めたい関数の微分]=0を満たすxとする必要(十分ではない)があるということである。
つまり、微分して次数が1次下がったの=0となるxを求めればよくて、
さらにそれを求めるには、同じように、と再帰的な操作を行うことで、取り合えずn次から2次まで次数を下げることが出来、
そこからまた一つずつ次数を上げていって詰めて行く、という方法をとったところ、かなりの精度でうまくいった。
でもこれでは複素解は求められない。あまり興味の湧かない話である。
◆弧と弦の長さから半径を求める
なんとなく丘とかの風景などを見ているとき、この丘は地面の下に埋まっている円弧の一部が現れたものだが、
果たして地面の下に埋まっているこの円の半径はどのくらいなんだろうか?と思ったことは無いだろうか(たぶん、ない)。
まあそんな愚かな問いを発してきた人物がいて、その夢を叶えたのが本プログラムである。
考えていると、sin関数を含んだ代数方程式が出てきて、どうしても解けなかった。
しかし、sinをテーラー展開することでn次代数方程式に帰着することが明らかになる。
ちょうど上のやつを作った後であったため、いきなり応用例が出てきてびっくりしたのを覚えている。
sinの展開の7次くらいまでやるとほとんど正確な値が出てくるのが分かった。
◆割と厳密な単振子
◆割と厳密な二重振子
微分方程式を扱うようなプログラムを作りたいナアと思って、真っ先に思いついたのが二重振子であった。
ていうか、この馴れ初めをぐだぐだ書く作業がなんかだるくなったため、もう止めにしようと思う。
二重振子の実験、これみるとなかなか面白いかもしれない。カオス的振る舞い。
前々からフラクタル図形というものに興味があって、よしやってみようと思って本とネットで調べながら作った。
意外ともの凄く簡単で、昨日一日で何時間かやっただけでまあまあそれっぽいのができて嬉しい(下図)。
こういった模様が機械的に算出されるのは面白い。一筆迷路はやめた。

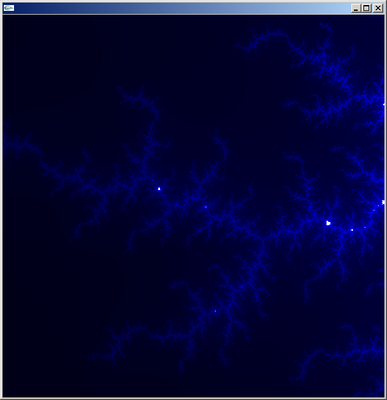


理論としてはzn+1=znk+Cという単純な漸化式を考えて、znの極限が発散しないようなCを複素平面上の点としてとるとできる。
特に、z0=0、k=2としたときに条件を満たすCの集合をマンデルブロ集合というらしく、今回はそれに従った。
左上の図形の一部分をある倍率で拡大してできたのが他の三つの図形(色は違うが)。
このように、図形に限らずとも、いくら拡大しても拡大しきれずに同じ性質を持つような、
部分と全体が自己相似になることをフラクタルというようです。非常にかっこいい言葉だと思う。
まあそんなことは調べればすぐ出てくるんでどうでもいいんですけど。
改良点ていうかこれに関連してやりたいこととして、
・計算回数による色のグラデーションの工夫
・Cの値も色に干渉するようにする
・漸化式の初期値や累乗の値を変える
・図形生成の高速化
・インターフェースをつくる
・別の数式から導かれるフラクタル図形を作る
・理論をもっと詰める
・自然に見られるフラクタルについて思いを馳せる
・フラクタル的存在としての自己について考察する
など。なんかもっといい画像が取れたらアップしようかと思う。
意外ともの凄く簡単で、昨日一日で何時間かやっただけでまあまあそれっぽいのができて嬉しい(下図)。
こういった模様が機械的に算出されるのは面白い。一筆迷路はやめた。
理論としてはzn+1=znk+Cという単純な漸化式を考えて、znの極限が発散しないようなCを複素平面上の点としてとるとできる。
特に、z0=0、k=2としたときに条件を満たすCの集合をマンデルブロ集合というらしく、今回はそれに従った。
左上の図形の一部分をある倍率で拡大してできたのが他の三つの図形(色は違うが)。
このように、図形に限らずとも、いくら拡大しても拡大しきれずに同じ性質を持つような、
部分と全体が自己相似になることをフラクタルというようです。非常にかっこいい言葉だと思う。
まあそんなことは調べればすぐ出てくるんでどうでもいいんですけど。
改良点ていうかこれに関連してやりたいこととして、
・計算回数による色のグラデーションの工夫
・Cの値も色に干渉するようにする
・漸化式の初期値や累乗の値を変える
・図形生成の高速化
・インターフェースをつくる
・別の数式から導かれるフラクタル図形を作る
・理論をもっと詰める
・自然に見られるフラクタルについて思いを馳せる
・フラクタル的存在としての自己について考察する
など。なんかもっといい画像が取れたらアップしようかと思う。
次のページ
>
PR
Profile
geroppii
Archive
