前々からフラクタル図形というものに興味があって、よしやってみようと思って本とネットで調べながら作った。
意外ともの凄く簡単で、昨日一日で何時間かやっただけでまあまあそれっぽいのができて嬉しい（下図）。
こういった模様が機械的に算出されるのは面白い。一筆迷路はやめた。

　
　

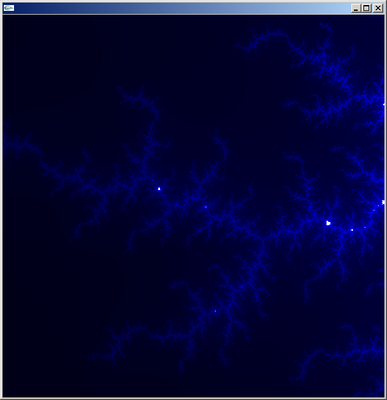
理論としてはz_n+1=z_n^k+Cという単純な漸化式を考えて、z_nの極限が発散しないようなCを複素平面上の点としてとるとできる。
特に、z₀=0、k=2としたときに条件を満たすCの集合をマンデルブロ集合というらしく、今回はそれに従った。
左上の図形の一部分をある倍率で拡大してできたのが他の三つの図形（色は違うが）。
このように、図形に限らずとも、いくら拡大しても拡大しきれずに同じ性質を持つような、
部分と全体が自己相似になることをフラクタルというようです。非常にかっこいい言葉だと思う。
まあそんなことは調べればすぐ出てくるんでどうでもいいんですけど。

改良点ていうかこれに関連してやりたいこととして、
　・計算回数による色のグラデーションの工夫
　・Cの値も色に干渉するようにする
　・漸化式の初期値や累乗の値を変える
　・図形生成の高速化
　・インターフェースをつくる
　・別の数式から導かれるフラクタル図形を作る
　・理論をもっと詰める
　・自然に見られるフラクタルについて思いを馳せる
　・フラクタル的存在としての自己について考察する
など。なんかもっといい画像が取れたらアップしようかと思う。